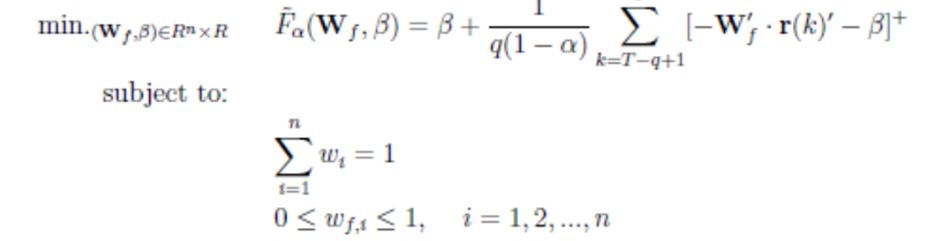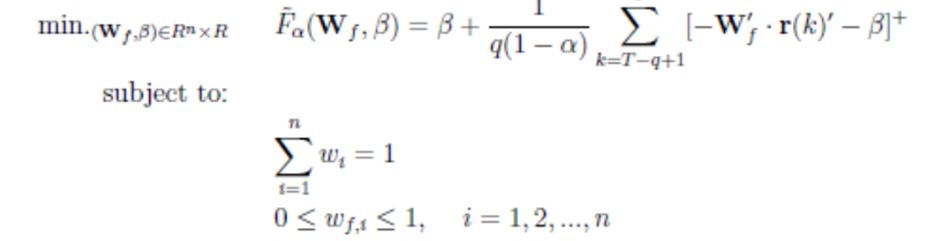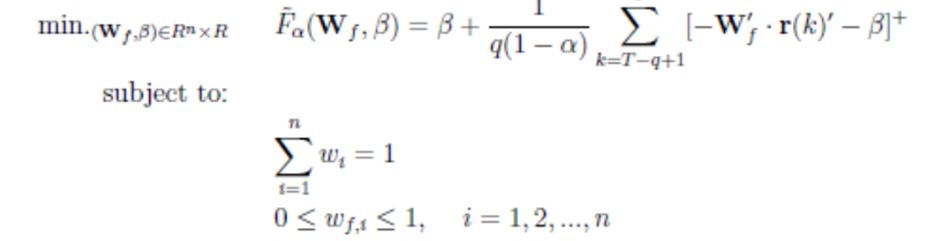PORTFOLIO CONSTRUCTION USING CVAR
投资组合优化:使用CVaR作为风险的度量
在构造投资组合的策略中,最小化风险(minimum volatility/minimum variance)是常用的算法。这类算法以数学优化为基础,将整体组合的风险作为目标函数或者约束条件,结合其他约束条件求解最优的投资组合。
虽然这种策略被广泛使用,值得注意的是它们存在着明显的缺陷。首先,把volatility/variance作为风险的度量是和假设投资产品(例如股票)的收益符合正态分布的相一致的。而事实证明股票的收益有两个明显的统计特征:不对称(asymmetry)和边缘分布(fat-tailed)。这两个特证不符合正态分布。另外,volatility/variance作为风险的度量并未区分有利的和不利(upside and downside)的风险,即,当我们控制投资组合的收益时,可能同时限制了正向的收益。
改进的风险度量有很多,本文首先讨论CVaR, conditional Value-at-risk。CVaR的定义和VaR的定义有密切的关联。假设以下的讨论中,VaR和CVaR的计算都从股票的历史数据中获得。
VaR(Value-at-risk):给定一个百分比alpha,VaR是在一定的时间段内,预期会在alpha为比例的时间内投资组合价值的最小损失,通常以百分比表示。VaR方法本身具有缺陷:VaR不满足一致性公理,即投资组合的风险不一定小于或等于该组合中各种资产分别计量的风险值之和,这与风险分散化的市场现象相违背;另外,VaR尾部损失测量的非充分性,它无法考察超过分位点的下方风险信息。
在给定以上的百分比alpha和计算所得的VaR值的前提下,CVaR指投资组合的损失大于某个给定的VaR值的条件下,该投资组合损失的平均值。与VaR相比,CVaR满足次可加性、正齐次性、单调性及传递不变性,是一种一致性的风险计量方法。
以下是VaR和CVaR的示意图。损失函数Loss的一个例子是收益的负数,即 –return。
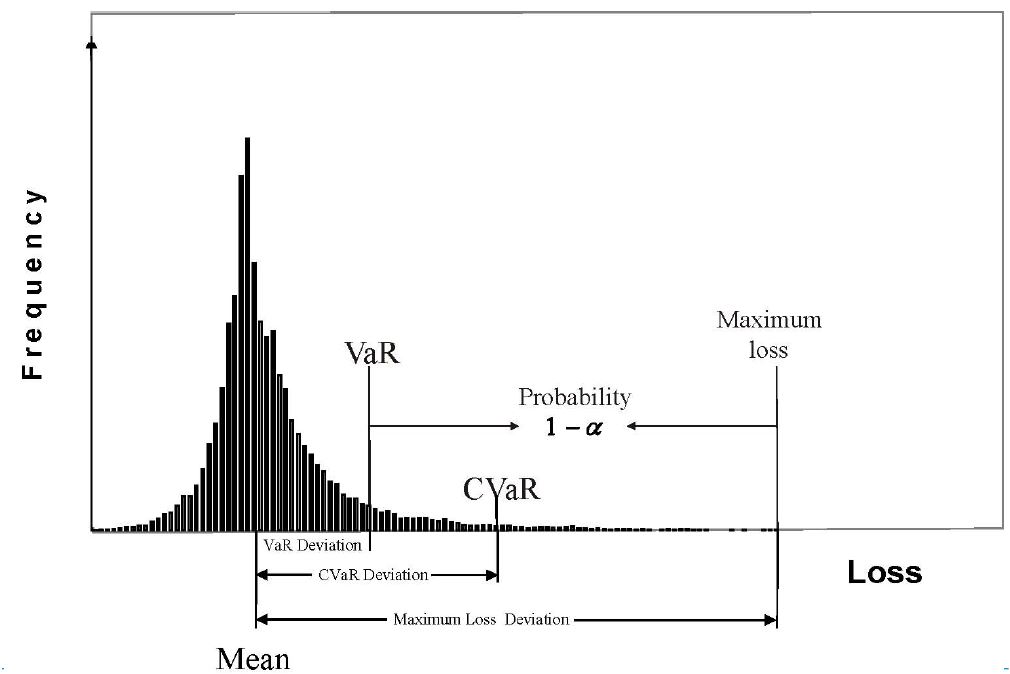 以python为例,计算股票历史收益stock_returns的VaR的代码如下。这里stock_returns是一个收益的时间序列。
以python为例,计算股票历史收益stock_returns的VaR的代码如下。这里stock_returns是一个收益的时间序列。
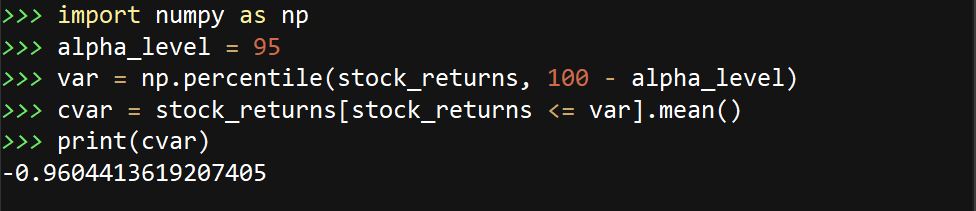
 计算股票收益的CVaR代码:
计算股票收益的CVaR代码:
 在投资组合的优化策略中,以最小化CVaR为例,将目标函数设为最小化投资组合的CVaR,约束条件为投资组合的权重非负,并且相加为1.0。Python的软件包scipy 提供scipy.optimize的minimize函数,将以上问题归结为一个非线性优化问题,而约束条件是线性的。
根据R.Tyrrell Rockfeller和Stanislav Uryasev的研究,参见文章‘Optimization of Conditional Value-at-Risk’,CVaR可以用一个线性函数作为近似。这样做的好处是,将上述的非线性优化问题转化为线性规划问题,不仅加快了运算速度,同时提高了求解的稳定性。
线性化以后的优化问题具有以下形式:
在投资组合的优化策略中,以最小化CVaR为例,将目标函数设为最小化投资组合的CVaR,约束条件为投资组合的权重非负,并且相加为1.0。Python的软件包scipy 提供scipy.optimize的minimize函数,将以上问题归结为一个非线性优化问题,而约束条件是线性的。
根据R.Tyrrell Rockfeller和Stanislav Uryasev的研究,参见文章‘Optimization of Conditional Value-at-Risk’,CVaR可以用一个线性函数作为近似。这样做的好处是,将上述的非线性优化问题转化为线性规划问题,不仅加快了运算速度,同时提高了求解的稳定性。
线性化以后的优化问题具有以下形式: